红黑树

红黑树是数据结构中一个难点的难点.数据结构的学习本来就比较难了，红黑树是又将难度上升一个档次的知识点

红黑树的规则

红黑树的规则：红黑树除了符合二叉搜索树的基本规则外，还添加了以下特性：

1. 节点是黑色或红色
2. 根节点是黑色
3. 每个叶子节点都是黑色的空节点(NIL节点)
4. 每个红色节点的两个子节点都是黑色节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

这些规则会让人一头雾水？
完全搞不懂规则叠加起来，怎么让一棵树平衡的.

红黑树的相对平衡

前面的约束，确保了红黑树的关键特性：

• 从根到叶子的最长可能路径，不会超过最短路径的两倍长
• 结果就是这个树基本是平衡的
• 虽然没有做到绝对平衡，但是可以保证在最坏的情况下，依然是高效的

为什么可以做的最长路径不会超过最短路径的两倍呢?

• 性质4决定了路径不能有两个相连的红色节点
• 最短的可能路径都是黑色节点
• 最长的可能路径是红色和黑色节点交替
• 性质5决定了所有路径都有相同数目的黑色节点
• 这就表明了没有路径能多余任何其他路径的两倍长

红黑树的变色

插入一个新节点时，有可能树不再平衡，可以通过三种方式的变换，让树保持平衡
换色、左旋转、右旋转

• 变色：为了重新符合红黑树的规则，尝试把红色节点换成黑色，或者把黑色节点换成红色

首先，需要知道插入的新的节点通常都是红色节点
因为在插入节点为红色的时候，有可能插入一次是不违法红黑树任何规则
而插入黑色节点，必然会导致一条路径上多了一个黑色节点，这是很难调整的
红色节点可能导致出现红红相连的情况，但是这种情况可以通过延申调换和旋转来调整

旋转

• 左旋转：逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己称为自己的左孩子
• 右旋转：顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取态，而自己称为自己的右孩子

插入操作

设要插入的节点为N(红色节点)，其父节点为P,祖父节点为G,父亲的同胞节点为U(叔叔节点)

情况一：新节点N位于树的根上，没有父节点

这种情况下，我们直接将红色变换成黑色即可，这样满足性质2(根节点为黑色节点)

情况二：新节点的父节点P是黑色

性质4(每个红色节点的两个子节点都是黑色==>从每个叶子到根的所有路径上不能又两个连续的红色节点)没有失效.
性质5(从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点)也没有任何问题.尽管新节点N有两个叶子节点NIL,但是新节点N是红色的，所以通过它的路径中黑色节点的个数依然相同.所以，不需要任何变换

情况三：新节点的父节点(P)是红色，叔叔节点(U)是红色(父红叔红祖黑)

(如果父节点是红色，叔叔节点也是红色，那么G（祖父节点）一定是黑色的)
解决方案=>把父(P)和叔(U)节点变成黑色，祖父(G)变成红色
操作方案：把P和U变换成黑色，并将G变换为红色
现在新节点N有了一个黑色的父节点P,所以每条路径上黑色节点的数目没有改变
而从更高的路径上，必然都会经过G节点，所以哪些路径的黑色节点数目也是不变的，符合性质5

可能存在的问题
但是N的祖父节点G的父节点也可能是红色，这就违反了性质4，我们可以递归的调整颜色
但是如果递归调整颜色到了根节点，就需要进行旋转了，待会我们的例子中会遇到这个问题

情况四：N的P(父亲)是红色,叔叔U是黑节点，且N是左孩子,祖父是黑色节点(父红叔黑祖黑，左孩子)

解决方法：父黑->祖红->右旋转

情况五：N的父亲P是红色的,叔叔U是黑色节点，祖父也是黑的，N是右孩子(父红叔黑祖黑，右孩子)

解决方法：以P为根左旋转=>将P作为新插入的红色节点考虑即可(情况四)=>父亲变成黑色=>祖红=>以祖为根右旋转

案例

题目：按10, 9, 8, 7, 6, 5, 4, 3, 2, 1顺序插入
插入的节点都是红色节点

第一次插入：插入10(红色节点)
第一次插入的为根节点=>情况一(新节点N位于树的根上，没有父节点)=>红色变成黑色
第二次插入：插入9(红色节点)
第二次插入父节点10是黑色节点=>情况二(新节点的父节点P是黑色)=>不需要任何变换
第三次插入：插入8(红色节点)
第三次插入父节点是9(红色节点)=>情况四(父红叔黑祖黑,左孩子)=>解决方法(父黑祖红，右旋转)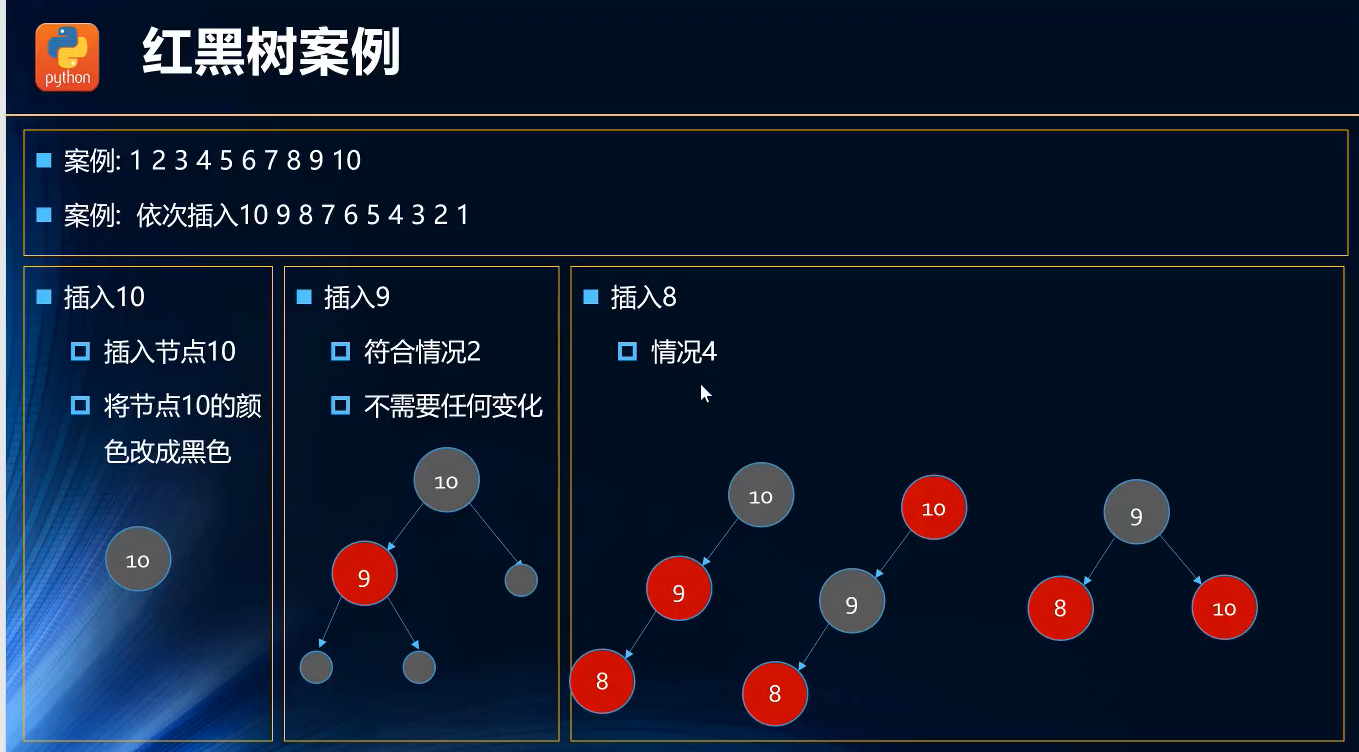

第四次插入: 插入7(红色节点)
第四次插入，父节点8是红色节点，叔叔节点10是红色节点=>情况三(父红叔红祖黑)=>解决方法(父黑叔黑祖红)=>(根节点9变成红色)不符合红黑树的规则二(根节点为黑色节点)=>只需要把根节点变成黑色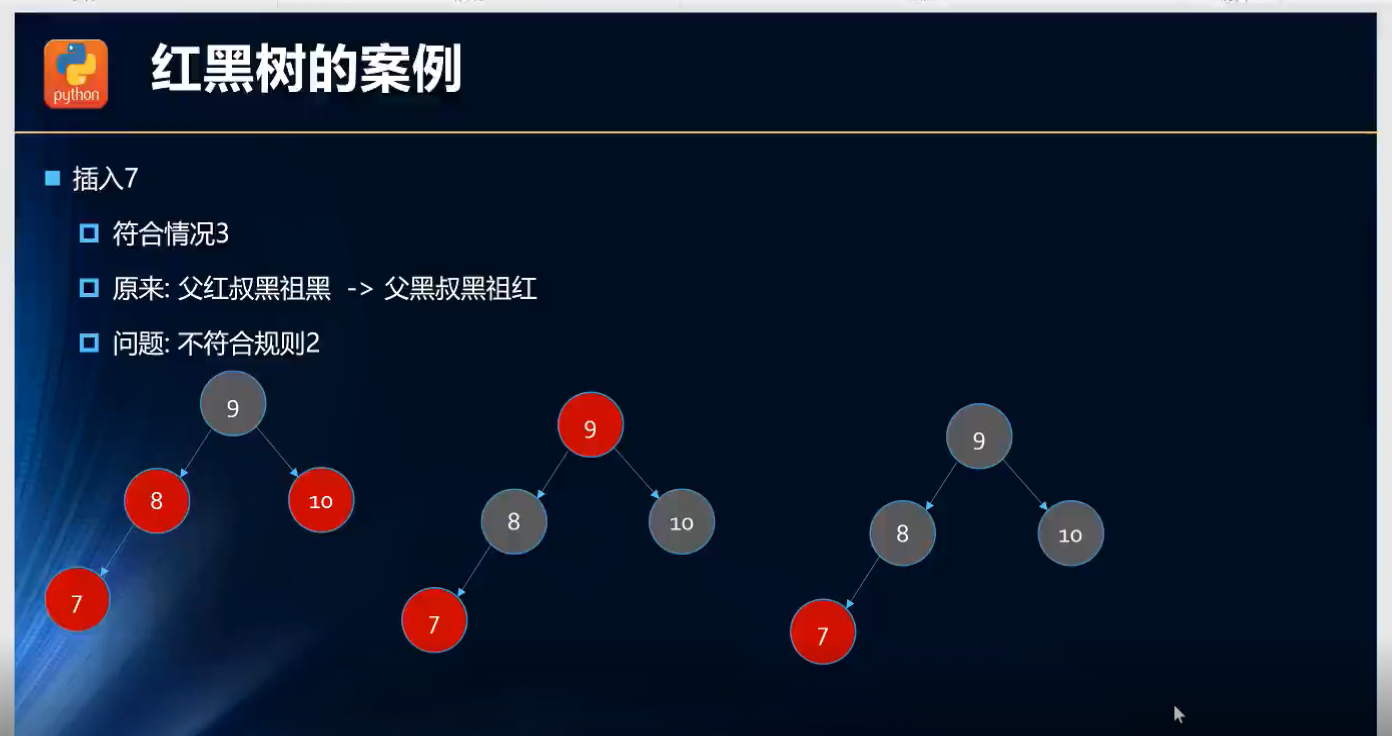
;

第五次插入：插入6(红色节点)
第五次插入，父节点是7(红色节点)，叔叔节点是NIL节点(黑色),祖父节点是8(黑色节点)=>情况四(父红叔黑祖黑，左孩子)=>解决方法(父黑祖红，右旋转)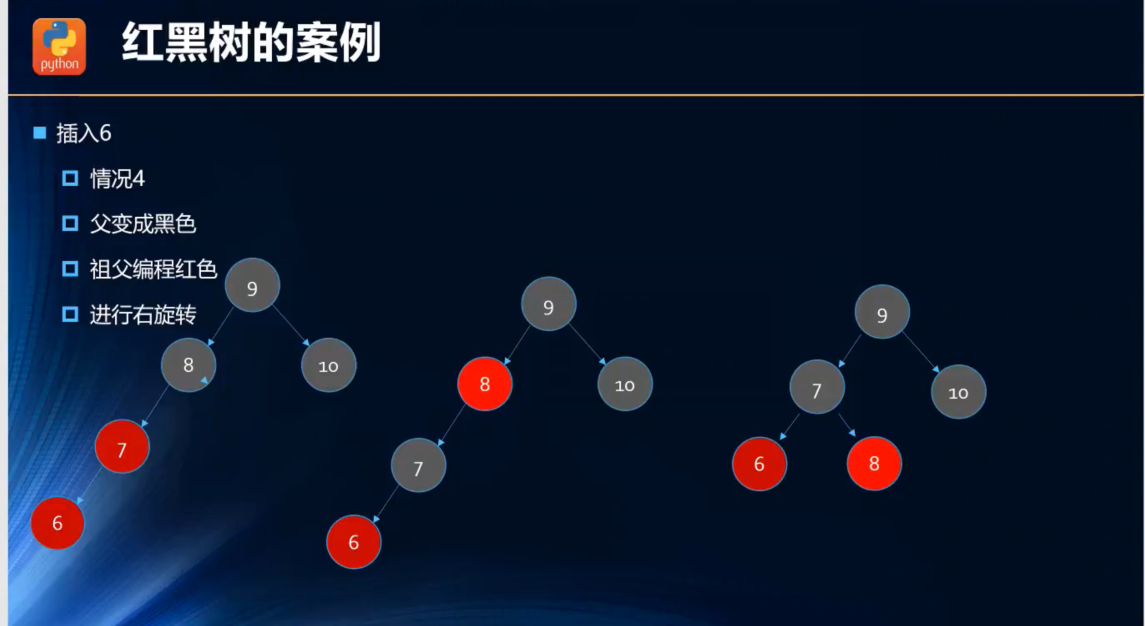
;

第六次插入：插入5(红色节点)
第六次插入，父节点是6(红色节点),叔叔节点8(红色节点),祖父节点7(黑色节点)=>情况三(父红叔红祖黑)=>解决方法(父黑叔黑祖红);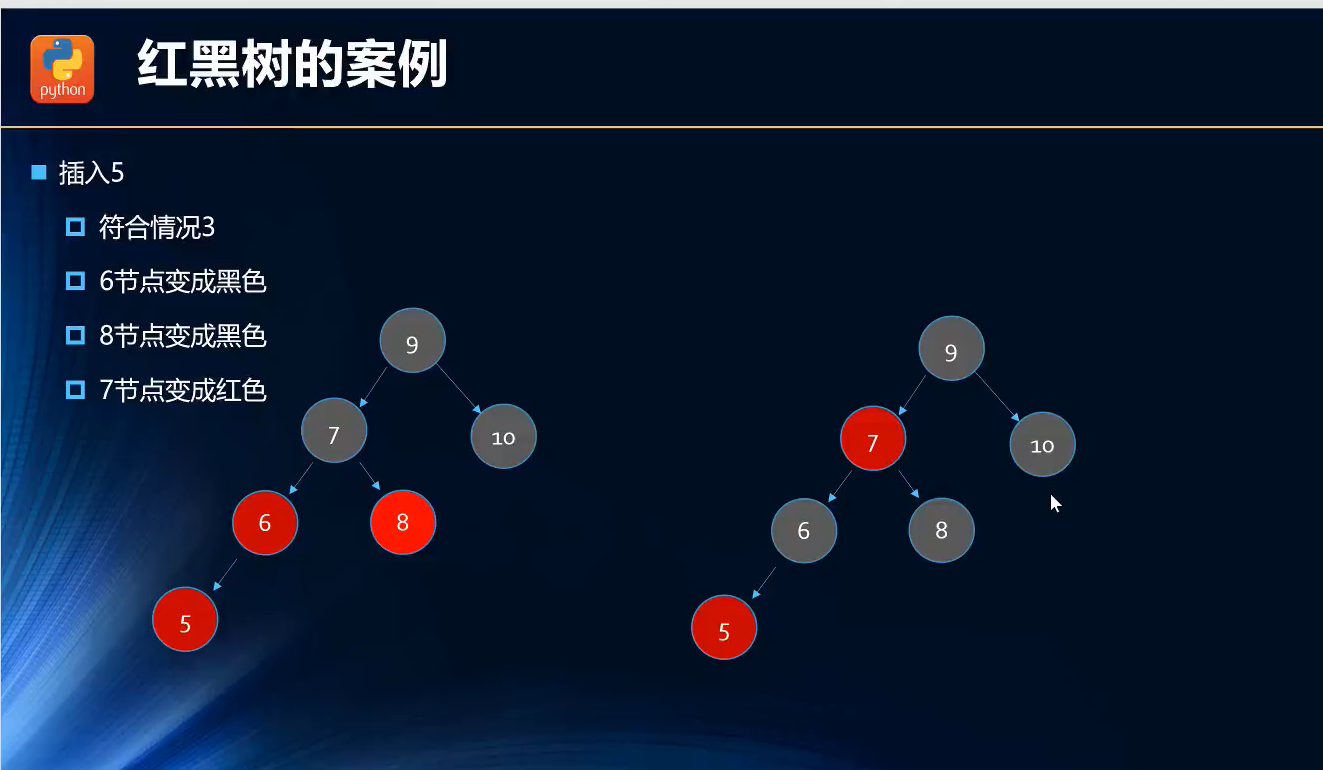
;

第七次插入：插入4(红色节点)
第七次插入，父节点是5(红色节点),叔叔节点是(NIL，黑色),祖父6(黑色)=>情况四(父红叔黑祖黑,左孩子)=>解决方法(父黑祖红，右旋转)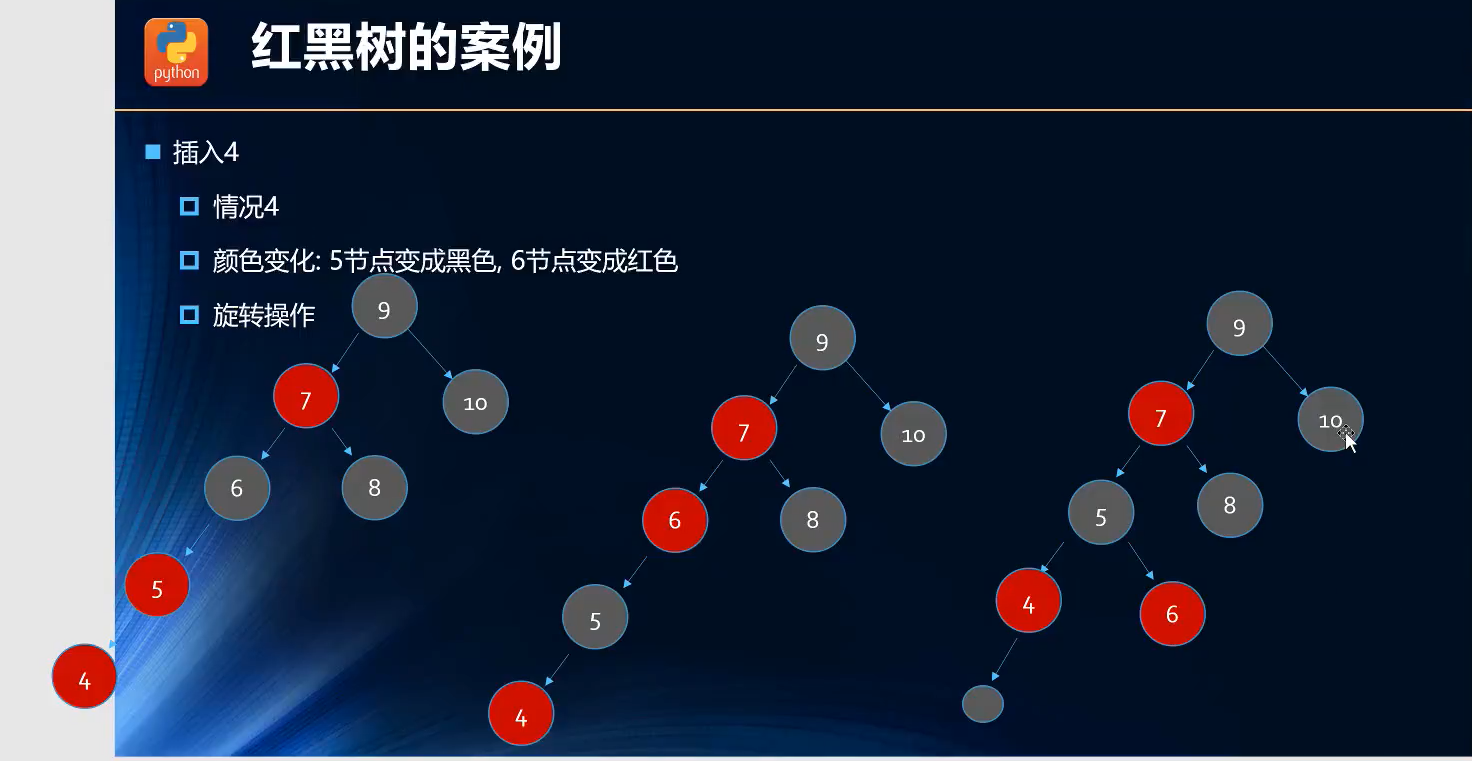
;

第八次插入：插入3(红色节点)
第八次插入，父节点是4(红色节点),叔叔节点是6(红色节点)，祖父节点是5(黑色)=>情况三(父红叔红祖黑)=>解决方法(父黑叔黑祖红)=>(存在问题，祖父变成红，祖父的父亲也是红的)=>情况四(看出一个整体，父红叔黑祖黑，左孩子)=>解决方法(父黑祖红，右旋转)=>右旋转时多了个8节点=>向右平移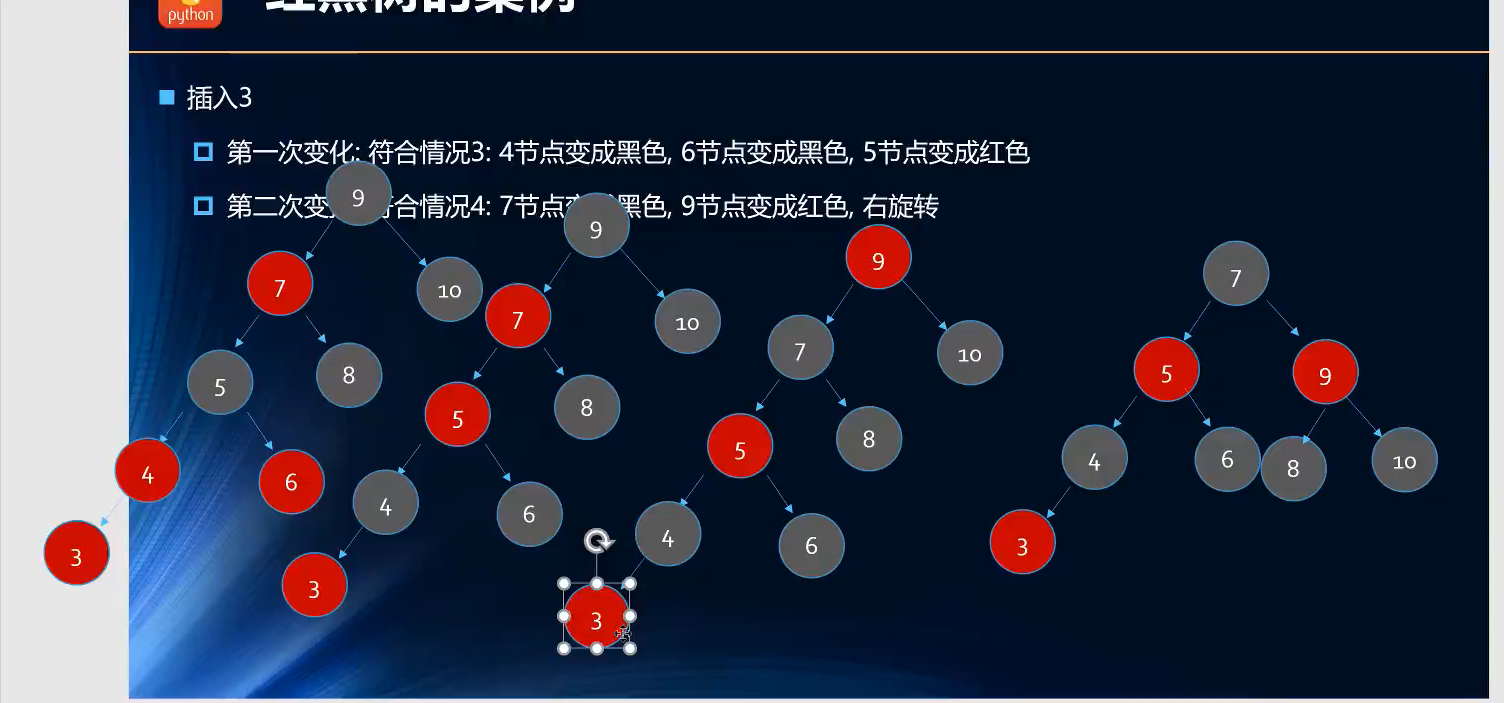
;

第九次插入：插入2(红色节点)
第九次插入，父节点是3(红色节点)，叔叔是NIL(黑色节点)，祖父是4(黑色节点)=>情况四(父红叔黑祖黑，左孩子)=>解决方法(父黑祖红，右旋转)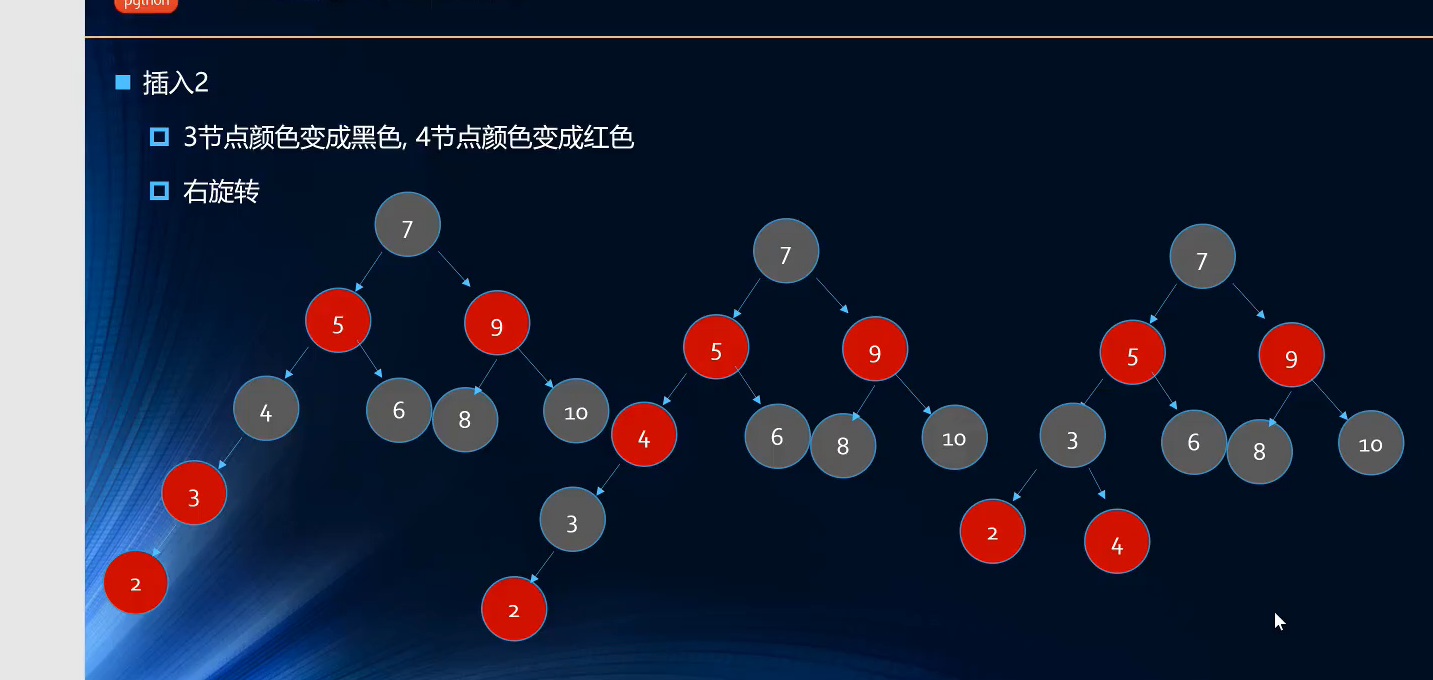
;

第十次插入：插入1(红色节点)
第十次插入，父节点是2(红色节点),叔叔节点是4(红色节点),祖父节点是3(黑色节点)=>情况三(父红叔红祖黑)=>解决方法(父黑叔黑祖红)=>(存在问题，祖父变成红，祖父的父亲也是红的)=>情况三(父红叔红祖黑)=>解决方法(父黑叔黑祖红)=>(存在问题,根节点变成红色)=>根节点变成黑色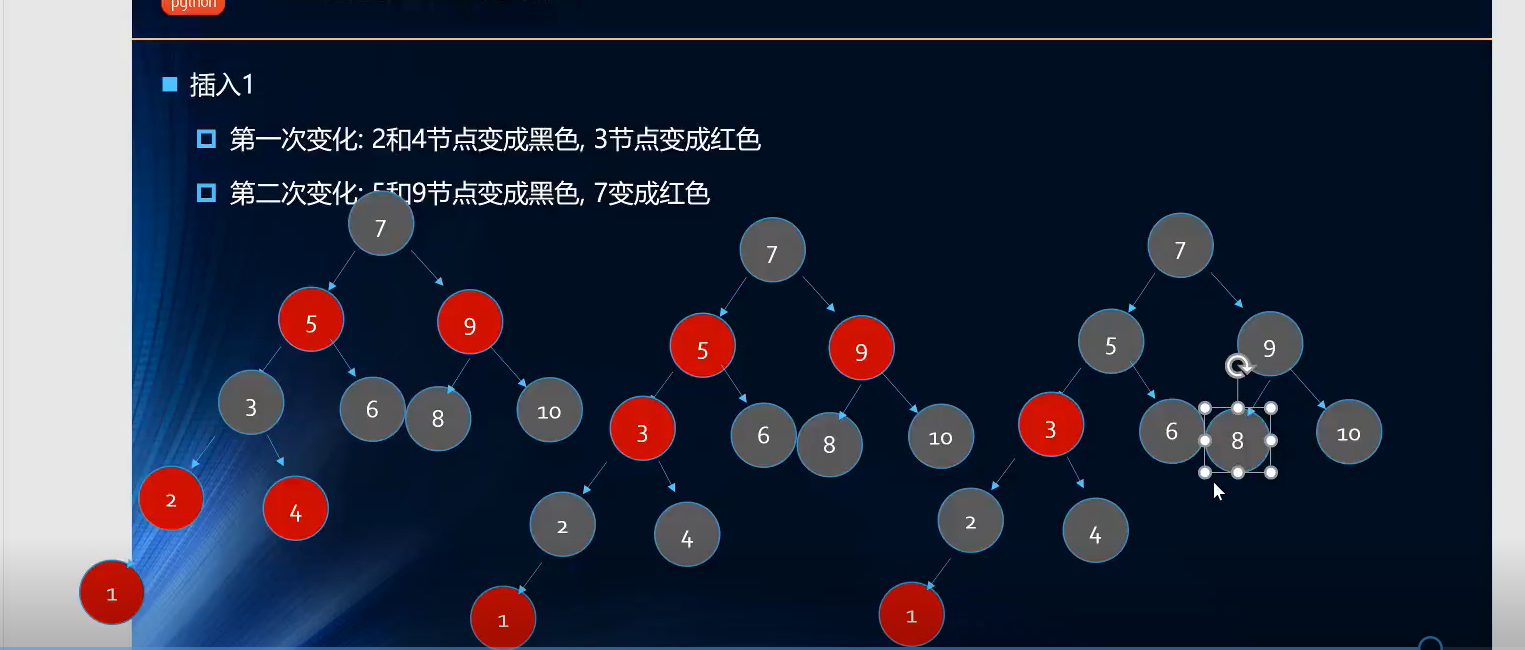
;

删除

红黑树的删除：我们学过二叉搜索树的删除操作，比较复杂，我们也学过红黑树的插入规则，比较复杂。

红黑树的删除操作呢？
就需要将两个复杂的操作结合起来考虑，所以难度非常大