希尔排序的思路
希尔排序是插入排序的一种高效的改进版,并且效率比插入排序要更快
插入排序的问题
假设一个很小的数据项在很靠右端的位置,这里本来应该是比较大的数据项的位置
把这个小数据项移动到左边的正确位置,所有的中间数据项都必须向右移动一位
如果每个步骤对数据项都进行了n次复制,平均下来是移动N/2,N个元素就是N*N/2=N^2/2
所以我们通常认为插入排序的效率是O(N^2)
如果有某种方式,不需要一个个移动所有中间的数据项,就能把较小的数据项移动到左边,那么这个算法的执行效率就会有很大的改进
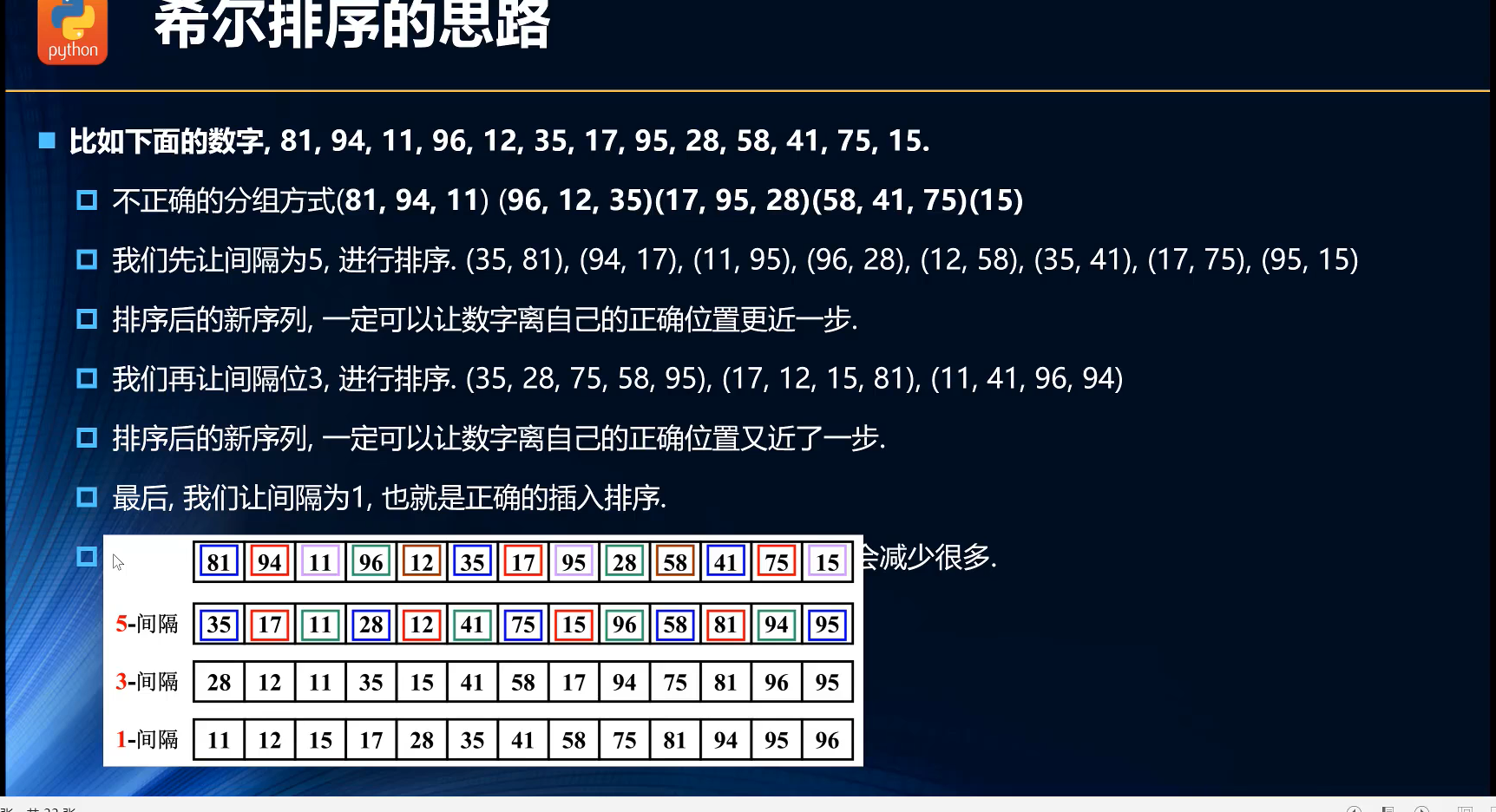
选择合适的增量
希尔原稿的做法
在希尔排序的原稿中,他建议的初始间距是N/2,简单的把每趟排序分成两半.也就是说,对于N=100的数组,增量间隔序列为:50 25 12 6 3 1.这个方法的好处是不需要在开始排序前为找合适的增量而进行任何的计算
Hibbard增量序列
增量的算法为2^k - 1 ,也就是1 3 5 7..等等.这种增量的最坏复杂度为
O(N^3/2),猜想的平均复杂度为O(N^5/4),目前尚未被证明
Sedgewick增量序列
{1, 5, 19, 41, 109, …}该序列中的项或者是94^i - 9*2^i + 1或者是4^i-32^i+1.这种增量的最坏复杂度为
O(N^4/3),平均复杂度为O(N^7/6),但是均未被证明
希尔排序的效率
希尔排序的效率和增量是有关系的.但是,它的效率是非常困难的,甚至某些增量的效率到目前依然没有被证明处理.但是经过统计,希尔排序使用元素增量,最坏的情况下时间复杂度为
O(N^2),通常情况下都要好于O(N^2)
总之,我们使用希尔排序大多数情况下效率都高于简单排序.这个可以通过统计排序算法的时间来证明.甚至在合适的增量和某些数量N的情况下,还好于快速排序